Weiertrass Approximation Theorem
Weiertrass Approximation Theorem :
Statement :
If f is a real continuous function defined on a closed interval [a,b] then there exists a sequence of real polynomials {Pₙ} which converges uniformly to f(x) on [a,b] i.e lim Pₙ(x)=f(x)
n-->∞
Proof :
If a=b , the conclusion follows by taking Pₙ(x) to be a constant polynomial ,
defined by Pₙ(x) = f(a) for all n .
We may thus assume that a<b . We next observe that a linear transformation
x' = (x-a) / (b-a)
is a continuous mapping of [a,b] onto [1,0] . Accordingly , we assume without loss of generality that a=0 , b= 1 .
Consider
F(x) = f(x) - f(0) - x[f(1) - f(0)] , for 0≤x≤1
Hence F(0) = 0= F(1) , and if F can be expressed as a limit of uniformly convergent sequence of polynomials , then the same is true for f , since f-F is a polynomial . So may assume that f(1)=f(0)=0 .
Let us further define f(x) to be zero for x outside [0,1] . Thus f is now uniformly continuous on the whole real line .
Let us consider the polynomial (non_ negative for |x|≤1)
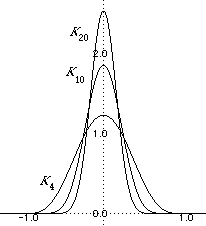
Bₙ(x) = Cₙ(1-x²)ⁿ , n= 1,2,3..... .....(1)
Where Cₙ is independent of x , is so chosen that
1
∫ Bₙ(x) dx = 1 for n= 1,2,3.... ....(2)
-1 1 1
∴ 1 = ∫ Cₙ(1-x²)ⁿ dx = 2Cₙ ∫ (1-x²)ⁿ dx
-1 0
1/√(n)
≥ 2Cₙ ∫ (1-x²)ⁿ dx
0
1/√(n)
≥ 2Cₙ ∫ (1-nx²) dx
0
= 4Cₙ / 3√(n) > Cₙ / √(n)
⇒ Cₙ < √(n) .......(3)
Which gives some information about the order of magnitude of Cₙ
Therefore , for any δ> 0 equation(3) gives
Bₙ (x) ≤ √(n)(1 - δ²)ⁿ , when δ≤|x|≤1.....(4)
so that Bₙ --> 0 uniformly for δ≤|x|≤1
Again let
1
Pₙ(x) = ∫ f(x+t) Bₙ(t) dt 0≤x≤1 .......(5)
-1
-x 1-x
= ∫ f(x+t) Bₙ(t) dt + ∫ f(x+t) Bₙ(t) dt
-1 -x
1
+ ∫ f(x+t) Bₙ(t) dt
1-x
For |x| ≤ 1, -1+x ≤ x+t ≤ 0 , for -1≤t≤-x , so that x+t lies outside [0,1] and therefore f(x+t) =0 , and hence the first integral on the right vanishes . Similarly , the third integral is also equal to zero . Hence
1-x 1
Pₙ(x) = ∫ f(x+t) Bₙ(t) dt =∫f(t)Bₙ(t-x)dt
-x 0
which is a real polynomial .
We now proceed to show that the sequence {Pₙ(x)} converges uniformly to f on [0,1] .
Continuity of f on the closed interval [0,1] .
Therefore , there exist M such that
M = sup |f(x)| ......(6)
and for any ε >0 , we can choose δ >0 such that for any two points x₁, x₂ in [0,1].
|f(x₁) - f(x₂)| < ε/2 , when
|x₁-x₂| < δ≤ 1 .....(7)
For 0≤ x≤ 1 , we have
1
| Pₙ(x) - f(x)|= |∫ f(x+t) Bₙ(t) dt - f(x)|
-1
1
= |∫ {f(x+t) - f(x)} Bₙ(t) dt|
-1
[using (2)]
1
≤ ∫ |f(x+t) - f(x)| Bₙ(x) dt
-1
-δ ( ∵ Bₙ(t)≥0)
= ∫ |f(x+t) - f(x)|Bₙ(t) dt
-1 δ
+ ∫ |f(x+t) - f(x)|Bₙ(t) dt
-δ
1
+ ∫ |f(x+t) - f(x)|Bₙ(t) dt
δ
-δ δ
≤ 2M ∫ Bₙ(t) dt + ε/2∫ Bₙ(t) dt
-1 -δ
1
+ 2M ∫ Bₙ(t) dt
δ
[Using equations(6) and (7)]
-δ 1
≤ 2M √(n)(1-δ²)ⁿ {∫ dt + ∫ dt }+ ε/2
-1 δ
[Using equations(2) and (4)]
≤ 4M √(n)(1-δ²)ⁿ + ε/2
< ε , for large values of n.
Thus for ε > 0 , there exists N (independent of x) such that
|Pₙ(x) - f(x)|< ε , ∀ n≥ N
⇒ lim Pₙ(x) = f(x) , uniformly on[0,1].
n-->∞
defined by Pₙ(x) = f(a) for all n .
We may thus assume that a<b . We next observe that a linear transformation
x' = (x-a) / (b-a)
is a continuous mapping of [a,b] onto [1,0] . Accordingly , we assume without loss of generality that a=0 , b= 1 .
Consider
F(x) = f(x) - f(0) - x[f(1) - f(0)] , for 0≤x≤1
Hence F(0) = 0= F(1) , and if F can be expressed as a limit of uniformly convergent sequence of polynomials , then the same is true for f , since f-F is a polynomial . So may assume that f(1)=f(0)=0 .
Let us further define f(x) to be zero for x outside [0,1] . Thus f is now uniformly continuous on the whole real line .
Let us consider the polynomial (non_ negative for |x|≤1)
Bₙ(x) = Cₙ(1-x²)ⁿ , n= 1,2,3..... .....(1)
Where Cₙ is independent of x , is so chosen that
1
∫ Bₙ(x) dx = 1 for n= 1,2,3.... ....(2)
-1 1 1
∴ 1 = ∫ Cₙ(1-x²)ⁿ dx = 2Cₙ ∫ (1-x²)ⁿ dx
-1 0
1/√(n)
≥ 2Cₙ ∫ (1-x²)ⁿ dx
0
1/√(n)
≥ 2Cₙ ∫ (1-nx²) dx
0
= 4Cₙ / 3√(n) > Cₙ / √(n)
⇒ Cₙ < √(n) .......(3)
Which gives some information about the order of magnitude of Cₙ
Therefore , for any δ> 0 equation(3) gives
Bₙ (x) ≤ √(n)(1 - δ²)ⁿ , when δ≤|x|≤1.....(4)
so that Bₙ --> 0 uniformly for δ≤|x|≤1
Again let
1
Pₙ(x) = ∫ f(x+t) Bₙ(t) dt 0≤x≤1 .......(5)
-1
-x 1-x
= ∫ f(x+t) Bₙ(t) dt + ∫ f(x+t) Bₙ(t) dt
-1 -x
1
+ ∫ f(x+t) Bₙ(t) dt
1-x
For |x| ≤ 1, -1+x ≤ x+t ≤ 0 , for -1≤t≤-x , so that x+t lies outside [0,1] and therefore f(x+t) =0 , and hence the first integral on the right vanishes . Similarly , the third integral is also equal to zero . Hence
1-x 1
Pₙ(x) = ∫ f(x+t) Bₙ(t) dt =∫f(t)Bₙ(t-x)dt
-x 0
which is a real polynomial .
We now proceed to show that the sequence {Pₙ(x)} converges uniformly to f on [0,1] .
Continuity of f on the closed interval [0,1] .
Therefore , there exist M such that
M = sup |f(x)| ......(6)
and for any ε >0 , we can choose δ >0 such that for any two points x₁, x₂ in [0,1].
|f(x₁) - f(x₂)| < ε/2 , when
|x₁-x₂| < δ≤ 1 .....(7)
For 0≤ x≤ 1 , we have
1
| Pₙ(x) - f(x)|= |∫ f(x+t) Bₙ(t) dt - f(x)|
-1
1
= |∫ {f(x+t) - f(x)} Bₙ(t) dt|
-1
[using (2)]
1
≤ ∫ |f(x+t) - f(x)| Bₙ(x) dt
-1
-δ ( ∵ Bₙ(t)≥0)
= ∫ |f(x+t) - f(x)|Bₙ(t) dt
-1 δ
+ ∫ |f(x+t) - f(x)|Bₙ(t) dt
-δ
1
+ ∫ |f(x+t) - f(x)|Bₙ(t) dt
δ
-δ δ
≤ 2M ∫ Bₙ(t) dt + ε/2∫ Bₙ(t) dt
-1 -δ
1
+ 2M ∫ Bₙ(t) dt
δ
[Using equations(6) and (7)]
-δ 1
≤ 2M √(n)(1-δ²)ⁿ {∫ dt + ∫ dt }+ ε/2
-1 δ
[Using equations(2) and (4)]
≤ 4M √(n)(1-δ²)ⁿ + ε/2
< ε , for large values of n.
Thus for ε > 0 , there exists N (independent of x) such that
|Pₙ(x) - f(x)|< ε , ∀ n≥ N
⇒ lim Pₙ(x) = f(x) , uniformly on[0,1].
n-->∞














Comments
Post a Comment
If Any Doubt Ask Me